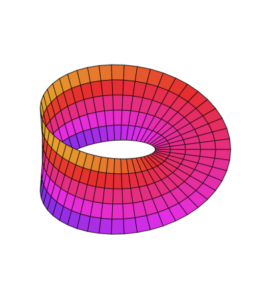
Title: Magical Mobius Strip: Unraveling the Mystery!
Description: Prepare to enter the world of twisted shapes as we explore the fascinating Mobius strip! In this experiment, you will create your very own Mobius strip—a unique mathematical object that has only one side and one edge. Discover the mind-bending properties of this enchanting shape as you learn about symmetry, topology, and the concept of infinity. Get ready to be amazed by the magic of the Mobius strip!
Scientific Principles:
- Symmetry: The experiment will introduce the concept of symmetry, showcasing how the Mobius strip has a twisted symmetry, unlike regular objects with bilateral symmetry.
- Topology: The Mobius strip demonstrates a topological concept called non-orientability, meaning it has no distinct “up” or “down” sides. You will learn about this fascinating property of the Mobius strip.
- Infinity: By exploring the Mobius strip’s infinite nature, you will gain an understanding of how the strip seems to have no end and how it challenges our perception of geometry.
Equipment Needed:
- Paper strip (about 1 inch wide and at least 12 inches long)
- Tape
- Scissors
- Markers or crayons for decorating (optional)

Difficulty Ratings: Equipment: ★☆☆☆☆ (1/5) Experiment: ★☆☆☆☆ (1/5)
Experiment Description:
- Gather all the materials listed above.
- Take the paper strip and hold one end in your hand.
- Twist the strip once by giving it a half-turn (180 degrees).
- Bring the ends of the strip together and align them.
- Secure the ends with a piece of tape to hold the shape in place.
- Congratulations! You have created your very own Mobius strip!
Optional Step: If desired, use markers or crayons to decorate your Mobius strip with colors and patterns.
Now, take a pencil and start tracing a line along the Mobius strip, starting from the middle. Observe as the pencil travels along both sides of the strip, covering the entire surface without ever lifting the pencil or reaching an end. This magical property demonstrates the unique nature of the Mobius strip.
Have fun exploring the symmetry, topology, and infinite possibilities of the Mobius strip. It’s an adventure into a world where shapes can twist and turn in unexpected ways. Get ready to unravel the mystery of the Mobius strip and discover the wonder of mathematics!
Simple Explanation:
The Mobius strip is a special twisted shape that has only one side and one edge. When we twist a strip of paper and connect the ends together, something magical happens! As we draw a line on the strip, it travels along both sides without ever reaching an end. It’s like taking a never-ending journey on a twisted road. This happens because the Mobius strip has a special twist that gives it the power to confuse our minds and make us believe it has no beginning or end!
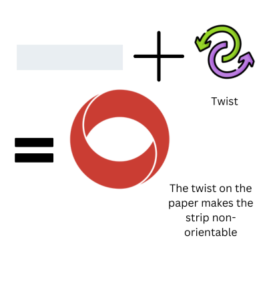
Detailed Explanation:
The Mobius strip is a fascinating mathematical object with some mind-bending properties. When we take a strip of paper and give it a half-twist before connecting the ends, we create a Mobius strip. This twist creates a unique shape that has some intriguing characteristics.
The Mobius strip is non-orientable, which means it doesn’t have a distinct “up” or “down” side. When we trace a line along the strip, we cover the entire surface without ever crossing an edge. This happens because the Mobius strip has only one side and one edge. As we traverse the strip, we move from one side to the other without realizing it, as the surface seems to blend seamlessly.
The Mobius strip’s non-orientability is a result of the twist in its structure. By adding that twist, we create a shape that challenges our intuition and perception of geometry. It’s an intriguing concept that explores the depths of topology, symmetry, and even the concept of infinity. The Mobius strip opens up a world of possibilities where shapes can twist and turn in unexpected ways, inviting us to explore the mysteries of mathematics.
Optional Follow-up Experiment: Cutting the Mobius Strip
Now that you have created your own Mobius strip, let’s continue the exploration by performing a fascinating follow-up experiment. We will cut the Mobius strip in two and three to observe the surprising results.
Materials:
- Two Mobius strips created from the previous experiment
- Scissors
Experiment Description:
- Take the Mobius strip you made earlier and examine its twisted shape.
- Cutting in Two: a) Start by holding one end of the Mobius strip and finding the middle point along its length. b) Use the scissors to carefully cut along the middle line of the Mobius strip. c) Observe what happens when you separate the strip into two parts. d) What do you notice about the resulting pieces? Are they the same or different? How many edges and sides do they have?
- Cutting in Three: a) If you want to take it a step further, find another middle point along the length of one of the pieces you obtained from the previous step. b) Use the scissors to cut along this new middle line, dividing one of the pieces into two. c) Again, observe the resulting pieces and analyze their characteristics. d) How do these new pieces compare to the ones obtained from the first cut? Do they still have the same properties?
This experiment will reveal some astonishing findings. By cutting the Mobius strip in two and three, you will discover that instead of getting two separate strips or three distinct parts, you end up with a larger number of interconnected loops. Even though you divide the strip, the Mobius strip’s unique properties persist, showing us that it’s not as simple as it seems.
Remember, be careful when using scissors, and always perform the experiment under adult supervision.

